RADIX OR BASE:-
※The number of values that a digit (one character) can have is equal to the base of the system.
※It is also called as the Radix of the system.
※ Base of Decimal (10),Hexadecimal (16),Binary (2) and Octal (8).
WEIGHT FOR DIFFERENT POSITION FOR A BINARY SYSTEM
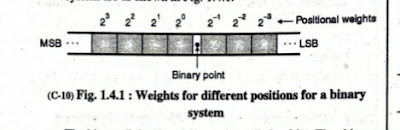 |
Column numbers to the right of the binary numbers start from -1 and become more and more negative(-1,-2,-3....)
CONVERSION FROM BINARY TO DECIMAL FORM
The general procedure for conversion from binary to decimal.
Steps to be followed:-
●Step 1) Note down the given number.
●Step 2) Write down the weight corresponding to different position.
●Step 3) Multiply each digit in the given numner with the corresponding weight to obtain product numbers.
●Step 4) Add all the product numbers to get the decimal equivalent.
Q1)
| 1 | 1 | 1 | 0 |
|---|
1*2^3 + 1*2^2 + 1*2^1 + 0*2^0
= 8 + 4 + 2 + 0
= 14
Ans:- (1110)B =(14)D
Q2)
↓ ↓ ↓ ↓ ↓
↓ ↓ ↓ ↓ ↓ ↓
| 1 | 1 | 1 | 1 | . | 1 |
|---|
1*2^3+1*2^2+1*2^1+1*2^0+1*2^-1
= 8 + 4 + 2 + 1 + 0.5
= 15.5
Ans:-(1111.1)B = (15.5)D
Q3)
| 1 | 0 | 1 | 0 | . | 1 | 1 |
|---|
1*2^3+0*2^2+1*2^1+0*2^0+1*2^-1+1*2^-2 = 8 + 0 + 2 + 0 + 0.5 + 0.25
= 10.75
Ans:- (1010.11)B = (10.75)D
Q4)
| 1 | 0 | 0 | 1 |
|---|
1*2^3 + 0*2^2 + 0*2^1 + 1*2^0
= 8 + 0 + 0 + 1
= 9
Ans:-(1001)B = (9)D
Q5)
| 1 | 1 | 0 | 0 | . | 1 |
|---|
1*2^3+1*2^2+0*2^1+0*2^0 + 1*2^-1
= 8 + 4 + 0 + 0 + 0.5
= 12.5
Ans:-(1101.1)B = (12.5)D
Extra questions:-
1) (1000.11)B → (8.75 )D
2) (0001)B → (01)D
3) (1010.11)B→( 10.75 )D
4) 1111.01)B →( 15.25 )D
5) (1110)B → ( 14 )D
6) (1001)B → ( 09)D




0 Comments
If you have any doubt,please let me know.